Deterministically Constrained Stochastic Optimization

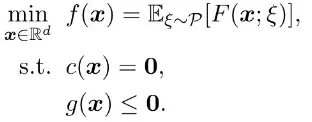
The above problem prominently appears in machine learning and statistics. For example, given $n$ response-feature data pairs $\{(b_i,\boldsymbol{a}_i)\}_{i=1}^n$, we can let $\mathcal{P} = \text{Uniform}(\{(b_i,\boldsymbol{a}_i)\}_{i=1}^n)$ be the empirical distribution. Then, $f$ reduces to the empirical loss $f(\boldsymbol{x}) = \frac{1}{n}\sum_{i=1}^n F(\boldsymbol{x}; b_i, \boldsymbol{a}_i)$, and we arrive at the $M$-estimation problems. The constraints that encode prior model knowledge are ubiquitous in practice. For example, in semiparametric estimation, we require the true parameter $\boldsymbol{x}^\star$ to satisfy $\boldsymbol{x}^\star\in\{\boldsymbol{x}\in\mathbb{R}^d:\|\boldsymbol{x}\|^2 = 1, \boldsymbol{x}_1>0\}$ to resolve the identifiability issue (Na et al., 2019, Na and Kolar, 2021).

Check out my highlighted works Na et al., 2022, 2023, Fang et al., 2022!