Statistical Inference of Stochastic Approximation

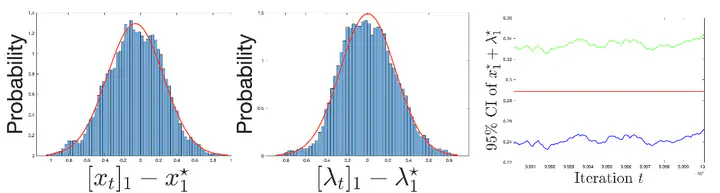
The first two plots show the histograms of the first-component error of the primal-dual iterates $\{(\boldsymbol{x}_t, \boldsymbol{\lambda}_t)\}_t$ generated by AI-StoSQP, and the third plot shows the $95\%$ confidence interval of $\boldsymbol{x}^\star_1+\boldsymbol{\lambda}^\star_1$ constructed based on $\{(\boldsymbol{x}_t, \boldsymbol{\lambda}_t)\}_t$. For more details, please refer to Na and Mahoney, 2022.

We denote $(\boldsymbol{x}^\star, \boldsymbol{\lambda}^\star)$ as the primal-dual solution to a constrained problem with a population loss function. Statisticians aim to construct estimators based on $n$ samples and infer properties of $(\boldsymbol{x}^\star, \boldsymbol{\lambda}^\star)$. Optimization people aim to design iterative stochastic approximation (SA) methods by realizing one sample at each step and demonstrate algorithmic convergence rates. Studying the limiting behavior of different SA methods bridges the gap between these two domains, enabling hypothesis testing and online construction of confidence intervals.