Long-horizon Nonlinear Optimal Control

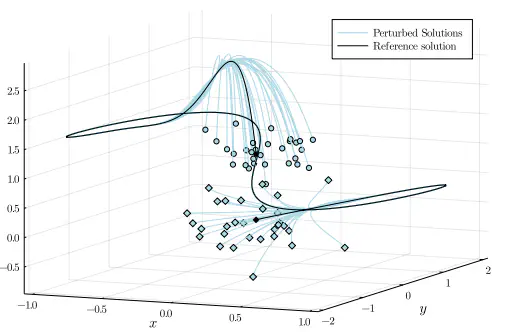
The figure above is taken from Na et al., 2022, which illustrates the robustness of the optimal state-control solution to system perturbations on the two boundaries, referred to as exponential decay of sensitivity in Na and Anitescu, 2020.

We focus on solving time-varying nonlinear optimal control problems (OCPs) given by: $$\begin{align} \min_{\boldsymbol{x}, \boldsymbol{u}}\;\; & \sum_{k=1}^{N-1} g_k(\boldsymbol{x}_k, \boldsymbol{u}_k) + g_N(\boldsymbol{x}_N),\\ \text{s.t.}\;\; & \boldsymbol{x}_{k+1} = f_k(\boldsymbol{x}_k, \boldsymbol{u}_k),\quad k = 0,\ldots,N-1,\\ & \boldsymbol{x}_{0} = \bar{\boldsymbol{x}}_0. \end{align}$$ We are particularly interested in OCPs with a large number of stages $N$, which typically arise in settings with long horizons, fine time discretization resolutions, and multiple timescales. By conducting sensitivity analysis of OCPs, we propose offline distributed methods and online real-time model predictive control (MPC) methods, demonstrating promising global and local convergence guarantees.

For more details, please check out my highlighted works Na and Anitescu, 2020, 2023, Na, 2021, Na et al., 2021, Na et al., 2022, Shin et al., 2022!