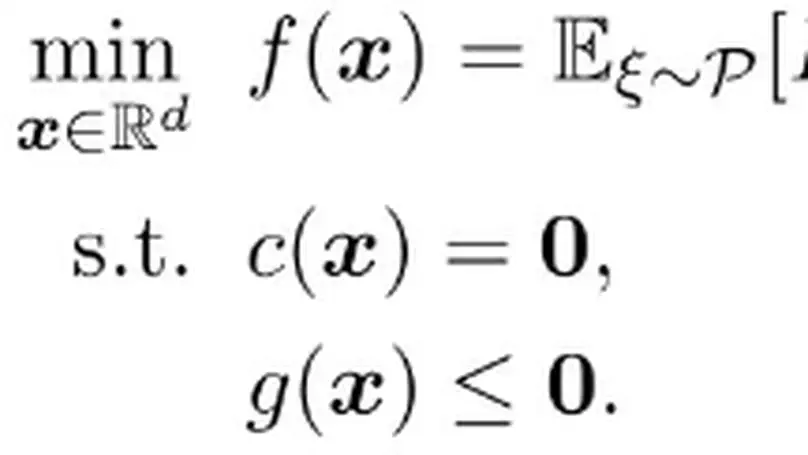I was trained as a statistician during my Ph.D. studies, but my postdoctoral research has expanded to encompass other areas, such as operations research, scientific computing, and industrial engineering. My research is rooted in the mathematical foundations of data science, with primary focuses on high-dimensional statistics, computational statistics, nonlinear and nonconvex optimization, and control. My ultimate research goal is to develop next-generation stochastic numerical methods that exhibit promising statistical and computational efficiency in solving various problems in scientific machine learning. These problems include scalable and reliable energy systems, safe reinforcement learning, physics-informed networks, algorithmic fairness, and more.

To achieve this, my research bridges modern statistics and classical optimization with a particular emphasis on various constraints and uncertainties. I develop practical methods by leveraging classical techniques from applied mathematics and numerical optimization, such as exact penalty, augmented Lagrangian, trust region, active set, and interior-point methods. I revisit, reform, and redesign these techniques to adapt them to special structures in modern statistical and decision-making problems, finally enabling me to address critical challenges such as scalability, reliability, and adaptivity.

Currently, my research focuses on the following concrete topics:

• Constrained stochastic optimization
• Statistical inference of stochastic second-order methods
• Machine learning with physics-informed constraints
• Stochastic real-time optimal control & model predictive control
• Semiparametric graphical models

There are three common threads in my research topics:

• I estimate the parameters of statistical models by optimizing certain loss functions that can only be evaluated in a noisy manner, typically through sampling/sketching.

• The model parameters must strictly adhere to hard constraints, which do not merely provide suggestions and lead to an inductive bias.

• The uncertainty quantification and online statistical inference of the developed methods are performed to determine estimation efficiency and draw statistically significant conclusions.

More specifically, my constrained problems have the following components:

• The model parameters $\boldsymbol{x}$ (or $\boldsymbol{\beta}$ as commonly used in statistics) can be in low, high, or infinite dimensions (e.g., a policy mapping in optimal control problems).

• The loss functions can be in purely stochastic form $E[f(\boldsymbol{x};\xi)]$, empirical finite-sum form $\sum_{i=1}^{n}f_i(\boldsymbol{x})/n$, or integral form $\int (\boldsymbol{x}(t) - \boldsymbol{x}_{ref}(t))^2 dt$.

• The constraints on the model parameters can be in equality, inequality, deterministic, or expected forms. Additionally, the model parameters can be restricted to some Riemannian manifolds or satisfying some PDEs.